引言
二千零八年五月十二日下午二點二十八分,四川省發生8.0級大地震,將近七萬人死亡,造成兩岸華人巨大的恐慌。隔天,有人在網路上公布淡江大學福園鯉魚池的神奇現象-上百隻鯉魚不停地繞圈圈,如圖一所示。無論怎麼用飼料引誘它們,都無法打破它們這樣持續一個月的行為。網路上眾說紛云,有人說是發生大地震的前兆,也有人說是魚類求偶的儀式,更有人說牠們在慶助馬英九坐上總統大位。最後,校方請來鯉魚專家解釋這異相-魚池的換水過濾器壞了,缺少活水注入,導致鯉魚缺氧,牠們才會不停地繞圈圈。
循環磨(Circular Mill)
1921年美國博物學家畢比(William Beebe, 1877-1962),在圭亞那(Guyana)叢林便曾目睹類似的現象。當時他發現有一大群螞蟻圍成一圓周約1200英呎的大圈圈爬行,每隻螞蟻至少花兩個半小時才能走完這一大圈。這些螞蟻就這樣盲目地繞了兩天,直到大部分螞蟻力竭身亡,大蟻圈逐漸被打破,倖存的螞蟻才開始找尋其它路徑,此現象被後來的生物學家稱為循環磨(Circular Mill)。生物學家之後在不同實驗室培養的蟻巢中發現相同現象,也發現魚群偶爾也會形成類似的群體行為[2],如圖二所示。 |  |
圖二、左圖為蟻群循環磨示意圖;右圖為魚群循環磨示意圖。[2]
螞蟻、魚類與鳥類等群居生物,由於個體觀察範圍有限,為了獵食或反獵食等生存目的,跟隨有限範圍中的同類是最簡單且有效的方法。雖然在極少數情況下,簡單的法則亦可能失誤,而導致循環磨這般盲從的結果(事實上即使號稱具有獨立思考能力的人類,偶爾也會出現盲從行為[3]),但在一般情況下,簡單的法則便足夠牠們成功完成相當複雜的工作。
費洛蒙式的協同行動(Stigmergy)
費洛蒙式協同行動是由法國生物學家格拉斯(Pierre-Paul Grassé)於1959年提出,解釋白蟻如何利用簡單法則,建構複雜且高大的蟻丘,如圖三。

圖三、兩座大城堡是白蟻們的傑作。[4]
首先,每隻白蟻只是團團轉地跑來跑去,漫無次序地用嘴銜起土粒又隨意放下。漸漸地,有些土粒開始碰巧地堆疊在一起成為微小土堆,如圖四,接著奇妙事情便發生了!

圖四、白蟻們一開始胡亂忙成一團,其實有特殊用意的。[5]
白蟻們開始持續地將土粒疊放在這些微小土堆上,如蓋柱子一般,瘋狂地堆高土粒,到達一定高度後,柱子開始傾斜並與其它柱子交疊,形成拱券式房間,一間間的套房就如此自然形成,並成為複雜且壯觀的蟻丘,如圖五所示。令人驚嘆的是,上述的建構過程,居然不是來自建築師或藍圖的幫忙!人們一直很難理解,沒有任何領導的低等動物,究竟如何有效分工完成複雜的事情呢?

圖五、白蟻蓋蟻丘示意圖。[5]
格拉斯發現大自然賦與螞蟻一種神奇天賦-費洛蒙,螞蟻只要善加利用這種天賦與同類互動,便可完成人類看來十分複雜的工作。蓋蟻丘的過程中,每隻白蟻銜起地上土塊時,便會在土塊上留下些許費洛蒙,並且遵循簡單原則堆放嘴中土塊-把土塊放在費洛蒙濃度最高的土堆上,若無法分辨哪裡最高,便隨機選擇一處。簡單法則看似平淡無奇,但互動過程卻是有效又複雜的。因為每一次白蟻的行動,都是一項正回饋(Positive Feedback),而正回饋的最後結果,就是把每隻白蟻動態地引導至正確位置。
自我組織行為(Self-Organizing Behavior)
個體透過簡單規則互動而突現(emergent)複雜有組織的群體現象,被稱做自我組織行為。利用自我組織方式,螞蟻還可以總是找到巢穴附近最豐富的食物來源地,並迅速找出巢穴與食物間最短的爬行路徑。然而,自我組織行為不僅存在螞蟻、鳥與魚群等群居生物世界,事實上近二、三十年來,許多不同領域的科學家幾乎同時發現自我組織的複雜行為,從分子、神經元、細胞、群居動物、社交網路(Social Network)、群眾行為到複雜的經濟活動都可以發現此類突現模式。1984年有一小群來自美國羅沙拉摩斯(Los Alamos)國家實驗室(因曼哈頓計劃而成立,世界最大實驗室之一)的科學家,為發現此突現模式感到興奮,甚至認為這將是繼牛頓古典物理學以來最大的科學革命,進而成立聖塔菲研究院(Santa Fe Institute),認為只要是與強烈互動有關的學問,都將是他們研究範圍。組成成員來自物理學、化學、電腦科學、經濟學、生物學、人類學等領域,其中更不乏多位諾貝爾獎得主,他們深信,他們正在開創二十一世紀新科學。然而創立之初的兩、三年,這群科學家雖有明確的研究方向-複雜系統(Complexity System),但始終無法簡明扼要的形容這門新科學,直到蘭頓(Chris Langton)出現。混沌的邊緣(The edge of Chaos)
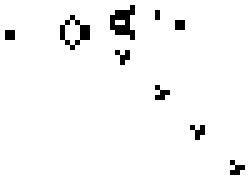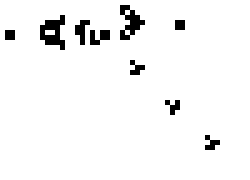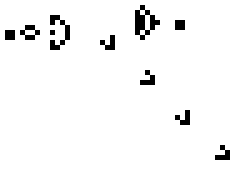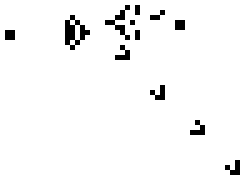 |  |
| (a)生命遊戲[6] | (b)細胞自動機突現的多樣型態[7] |
圖六、生命遊戲與細胞自動機
起初蘭頓只是從觀察中記錄數個具有自我複製能力的形態,但仍然無法從中歸納出他們共同的特性,儘管如此,蘭頓仍樂此不疲地研究著這些格子。直到有一天他看到天才物理學家沃富仁(Stephen Wolfram)歸納的四種細胞自動機類型,他才發現自己可能欠缺動力系統及混沌的相關知識,並在鑽研這些書籍文獻的同時,也開始調控細胞自動機的系統參數,觀察系統產生的整體行為。
直到有一天,他發現系統參數存在著某個臨界值,當參數小於臨界值時,系統會產生死寂般的停滯塊狀;而參數大於臨界值時,系統便出現混沌狀態。唯有參數維持在此臨界值時,秩序與混沌的勢力相當,結構不斷地成長、分裂、重組,並流動著花式複雜的樣貌。蘭頓發現這現象時大為震撼,因為這與物質二級相變的過程相當類似。從此,蘭頓便開始猜想生命或許便是由這種混沌與秩序拉扯下而突現的某種平衡,並為這類動態平衡的概念命名,稱作「混沌邊緣」。日後,蘭頓到聖塔菲實驗室做博士後研究,「混沌邊緣的突現」有如畫龍點睛般,為複雜科學烙下最初的定義。
人工生命(Artificial Life)
蘭頓的偉大發現,使他心中開始萌生一個堅定信仰-生命就是一種計算的形式。因此他有個更大的企圖心,他想從電腦中捕捉更多具有生命本質或演化的抽象模型。當時他興高采烈地將此想法向生物學家及電腦科學家尋求認同,卻總是吃上閉門羹。即是在學術資料庫廣泛地搜尋,找到的相關研究也非常有限,偶爾難得找到幾篇令人興奮的論文,卻總是出現在奇怪、冷僻的領域。但他相信世界上某些角落,肯定存在一些擁有類似想法,仍在摸索研究方向,又苦無知音的寂寞靈魂。於是蘭頓決定創辦一個國際研討會來凝聚這些人,一同創辦一門真正的新科學-人工生命。人工生命與人工智慧很類似,但有更大的企圖心,它不是用電腦來模擬思考過程,而是用電腦模擬基本的生物演化方式及生命本身。 柏茲模型(Boids Model)
1987年9月,蘭頓在羅沙拉摩斯籌備的第一屆國際人工生命研討會,得到了廣泛的迴響,共一百五十多名來自世界各地從事相關研究的學者與記者參加。各國學者在會議中都興致勃勃且迫不及待地展現自己獨自摸索多年的寶貝,有人談模擬演化的計畫、有人談胚胎發育的模擬演化、也有人談機器人,不過都沒有雷諾茲(Craig Reynolds)的柏茲模型讓人印象深刻。雷諾茲從麻省理工學院拿到碩士文憑後,便一直在業界的繪圖部門從事二維與三維動畫的系統設計與研究。工作期間,他驚訝地發現他僅需賦與系統中的柏茲(類鳥,bird-oid)三種簡單的互動規則,並任這些柏茲自由互動,便可輕易地產生擬真的鳥群飛翔行為。1987年7月,雷諾茲將其研究成果發表在電腦圖學最頂級的學術研討會上(ACM SIGGRAPH),產生了極大的迴響,日後並被電腦圖學研究者公認為電腦群體動畫的始祖,今日大家耳熟能詳的魔戒等魔幻史詩般電影大場景,便是利用這類技術所完成。然而雷諾茲的柏茲模型,真正在生物學、物理學、計算社會學、經濟學、機器人學、控制學等眾多領域開始留下深刻印象,是在兩個月後,蘭頓的國際人工生命(Artificial Life)研討會。
雷諾茲受邀於蘭頓,在人工生命研討會上展示他的柏茲模型。柏茲模型中的每隻柏茲(boid),皆具有一個有限的視野範圍並賦與自主運動的能力,當其它柏茲進入自己的有限視野範圍時,便遵循三個簡單的區域性規則(local rule)與其它的柏茲互動[8],如圖七:
1. 避免碰撞(Collision Avoidance): 與鄰近的柏茲保持一個最小距離,以避免碰撞。
2. 對齊速度(Velocity Matching): 和鄰近柏茲的平均速度盡量保持一致。
3. 向中心凝聚(Flock Centering): 向鄰近柏茲的平均位置移動。
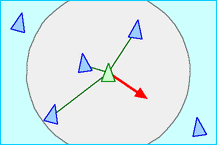 | 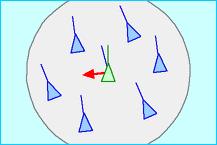 | 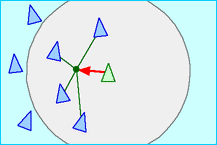 |
| (a)避免碰撞 | (b)對齊速度 | (c)向中心凝聚 |
圖七、柏茲遵循的三種簡單區域性互動規則。[9]
電腦模擬開始時,雷諾茲讓柏茲全完隨機散布在電腦螢幕上。緊接著,兩兩相鄰的柏茲便開始一同飛行,並沿路聚集其它的柏茲,自然而然地形成群體飛行的姿態。即使環境中有障礙物,他們也會自動地暫時分開以避開障礙物,並在閃過障礙物後會合、如圖八所示。偶爾柏茲難免撞上障礙物,在原地轉了幾圈而失去方向,不過一旦其它柏茲從旁飛過,它便會立刻重新加入飛行的隊伍,一切看起來都相當地自然。
當時,研討會的學者們皆目不轉睛地盯著電腦螢幕上飛行的柏茲群體,一方面想確認眼前的群體行為是否可能露出事先透過程式腳本規劃的蛛絲馬跡;另一方面,心想這群柏茲若真無任何監控,僅靠三個簡單的區域法則,便可自發地形成這般複雜群體行為,這將是自我組織、複雜系統最生動、最具說服力的例證!
儘管近年的統計物理學者發現真實世界的鳥群,溝通方式與雷諾茲的柏茲模型並非完全相符[11]。但這毫無損及雷諾茲當年的貢獻,因為柏茲模型已將複雜理論的精神深深烙印在各領域學者的腦海中,並充分展現了簡單就是美的真理。
新的生命觀點
第一次國際人工生命研討會的成功,象徵著人工生命研究領域的正式誕生。蘭頓認為人工生命與傳統生物學恰好是背道而馳,人工生命不是用分析法來解析生命,後者把生物體系分成物種、有機體、器官、組織、細胞及分子等,前者是企圖在人工系統中設計簡單的個體,並組合這些個體來創造近似生命的行為。此外,人工生命重視的是生命可能的形態(life-as-it-could-be),與傳統生物學所重視的已知的生命形態(life-as-we-know-it)有相當大的不同。因為傳統生物學僅是以地球上的生命為基礎所建立的一種實例,然而地球上的生物包括人類的出現,僅僅是最初地球上某種簡單物質所進化的一種結果,這樣的經驗並不能提供我們了解或創立宇宙普適的生命觀點。人工生命想要跳脫這思考侷限,期望藉由電腦或其它機器等新媒介來探索生命所有可能的形式;另一原因是,人工生命相信生命的本質在於形式而不在於具體的物質,只要能夠將物質本身的運作邏輯抽出,並將之賦與某個人工代理人(agent),然後觀察這些代理人彼此互動後所突現(emergent)的行為,便可能從中找到生命可能的形式。複雜來自簡單
從電腦的模擬過程中,愈來愈多學者發現,極其簡單的元素集合起來,就可能突然出現有趣且迷人的複雜行為。在研討會中,許多人都提到,要產生類似生命的行為,基本單位應愈簡單愈好,且系統中控制的參數應是基本單位的局部法則,而非直接控制群體全域的法則。因為生命是由下而上,透過基本單位彼此平行互動計算,自然而然所突現出的自我組織形態。筆者因研究需要,曾自行用程式實作了雷諾斯的柏茲模型,並額外賦與系統中每隻柏茲一個自主的向前推力,以解決柏茲落單時的停頓情形。結果發現系統中的柏茲們偶爾會自動圍成一個圈圈,並且不斷的繞行,形成一種動態的平衡,如圖九所示。
圖九、筆者實作的柏茲模型中偶爾突現的循環磨。
起先筆者一直以為是程式中存在著小臭虫(bug)所導致,後來無意間得知循環磨的生物現象,才發現它與筆者的模擬成因和互動結果是巧妙吻和的。二千零八年五月十三日,四川大地震的隔天,筆者在網路上看到淡大福園鯉魚瘋狂轉圈圈被說成地震的異象,後來更被鯉魚專家以缺氧一說作結。筆者嘗試向網友解釋循環磨現象與地震和缺氧無關,這僅是大自然自我組織行為的一種失誤特例,但仍不敵鯉魚專家的缺氧說簡單且更具一般說服力。不過筆著認為科學的核心就是說故事,解釋世界為何是現在所看到的樣子,儘管一般人並不總是願意聽完冗長的科學故事,但只要故事的題材有趣,可以被其它人接下去說並且愈說愈精彩,那麼這個故事就值得一說。
混沌邊緣的藝術-人工生命
二十世紀知名畫家-畢卡索(Pablo Picasso)曾說過一句名言:「我們都知道藝術不是真實,藝術是一則讓我們瞭解真實的謊言。」而人工生命何嘗不也是如此?
二十世紀知名畫家-畢卡索(Pablo Picasso)曾說過一句名言:「我們都知道藝術不是真實,藝術是一則讓我們瞭解真實的謊言。」而人工生命何嘗不也是如此?
參考來源與文獻
[1] 圖片來源:http://towel1988.pixnet.net/blog/post/17580322,
[2] T.C. Schneirla (1944) "A unique case of circular milling in ants, considered in relation to trail following and the general problem of orientation," American Museum Novitates, 1253:1–26.
[2] T.C. Schneirla (1944) "A unique case of circular milling in ants, considered in relation to trail following and the general problem of orientation," American Museum Novitates, 1253:1–26.
[3] S. Milgram(1963) "Behavioral Study of Obedience," Journal of Abnormal and Social Psychology 67: 371–378.
[4] 圖片來源:
http://onionesquereality.wordpress.com/2008/01/31/adaptive-routing-taking-cues-from-stigmergy/
http://onionesquereality.wordpress.com/2008/01/31/adaptive-routing-taking-cues-from-stigmergy/
[8] C. W. Reynolds (1987) "Flocks, herds and schools: A distributed behavioral model, " Proc. of the 14th annual con-ference on Computer graphics and interactive techniques, ACM Press, pp. 25–34.
[9] C. W. Reynolds (1999) "Steering behaviors for autonomous characters," Proc. of Game Developers Conference.
[11] M. Ballerini, N. Cabibbo, R. Candelier, A. Cavagna, E. Cisbani, I. Giardina, V. Lecomte, A. Orlandi, G. Parisi, A. Procaccini, M. Viale and V. Zdravkovic (2007) "Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study," Proceedings of the National Academy of Sciences of the United States of America.

很有趣的文章!:)
ReplyDeletethanks for the compliment. :)
ReplyDelete很棒的文章
ReplyDelete